
Czy topologia mikroobiektów może wpływać na ich ruch w środowisku? Eksperymenty i symulacje numeryczne naukowców z Polski i Szwajcarii opublikowane w czasopiśmie Physical Review Letters pokazują, że sposób opadania łańcuszków w lepkim płynie zależy od tego, jakiego rodzaju węzeł został na nich zapleciony. Opadając, łańcuszki mogą tworzyć płaskie toroidalne struktury złożone z kilku oplecionych pętli wirujących względem siebie. Motywacją do tych badań jest ich potencjalne znaczenie dla zrozumienia dynamiki zawęźlonych nici DNA i poznania związku pomiędzy topologią biomolekuł a ich kształtem i szybkością opadania pod wpływem grawitacji lub w wirówce.
W 1867 roku dwóch szkockich fizyków – Peter Tait i William Thomson (lord Kelvin) – badało ruch kółek z dymu wytwarzanych przez specjalnie skonstruowaną w tym celu maszynę. Uderzyła ich stabilność ruchu kółek – zaraz po powstaniu przybierały one spłaszczoną, toroidalną formę i przesuwały się bez dalszej zmiany kształtu.
 |
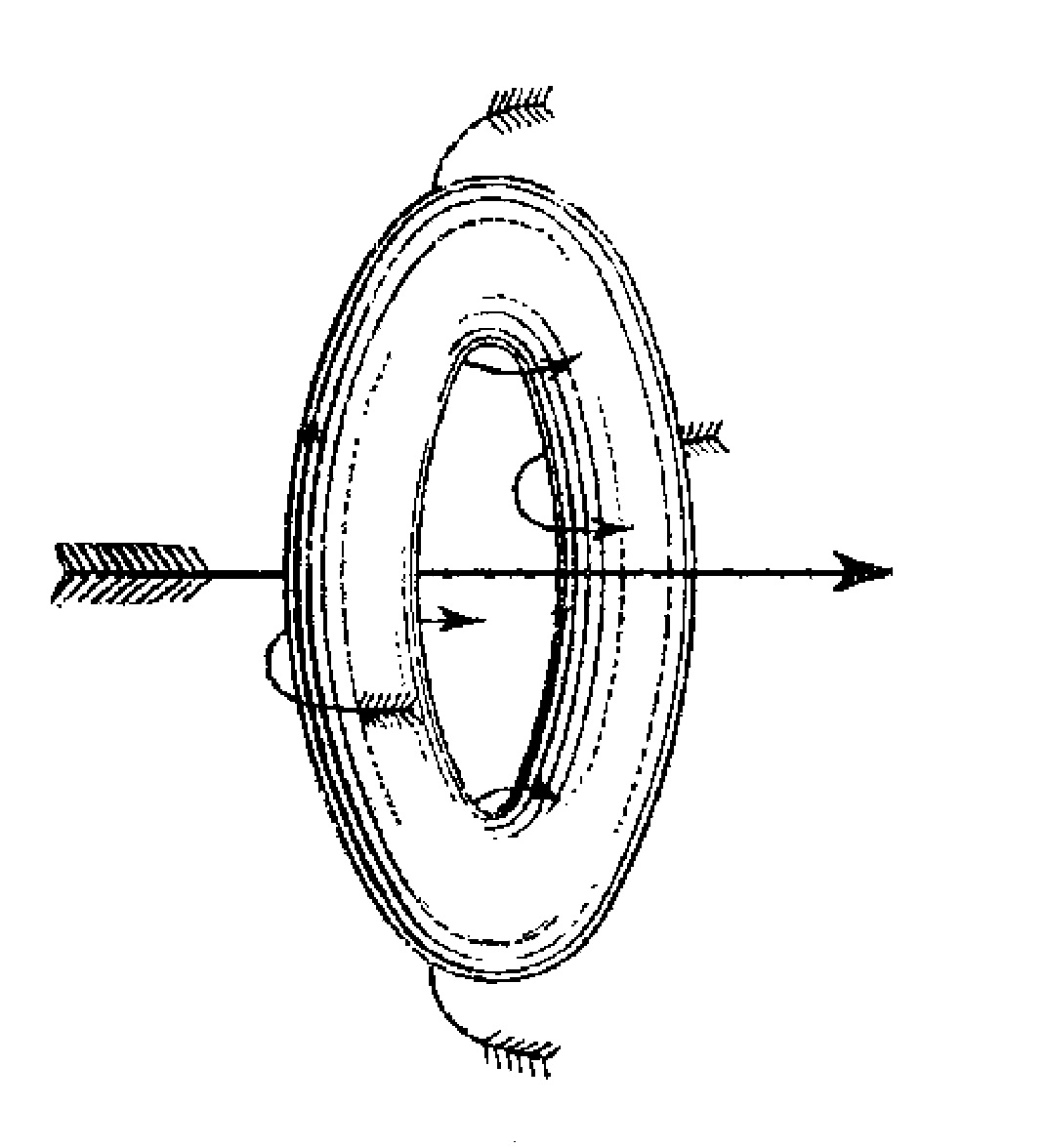 |
Rycina ilustrująca eksperyment Taita i wizualizacja ruchu powietrza wokół kółka z dymu (Peter Tait, Lectures on Some Recent Advances in Physical Science, MacMillan & Co., London, 1876)
Struktury te to w istocie swojej wiry pierścieniowe, w których oś wiru tworzy zamkniętą pętlę. Kelvin pokazał, że w pozbawionej oporów cieczy taki ruch wirowy utrzymywałby się dowolnie długo. W szczególności – jak przekonywał – gdybyśmy oś wiru zawiązali w węzeł, ten nigdy się sam nie rozwiąże. Może więc – myślał Kelvin – takie właśnie zasupłane wiry (tyle że w wypełniającym wszechświat eterze) są atomami, które tworzą pierwiastki? Różne sposoby zasupłania węzłów wirowych odpowiadałyby wtedy różnym atomom.
I chociaż koncepcja ta nie wytrzymała próby czasu, to jednak rozważania Kelvina i Taita stanowiły początki całej gałęzi współczesnej matematyki – teorii węzłów, stosowanej do modelowania obserwowanych w przyrodzie struktur topologicznych. Również i w fizyce węzły, sploty i inne układy o nietrywialnej topologii pojawiają się coraz częściej – m. in. w magnetohydrodynamice opisującej m. in. przepływy plazmy w okolicy Słońca, w schematach korekcji błędów w komputerach kwantowych, w kwantowej teorii pola czy w opisie ciekłych kryształów. Węzły spotykamy też w układach biologicznych, przede wszystkim w nici DNA, która jest tak długa, że często plącze się sama, jak kabel od słuchawek w kieszeni, i dopiero specjalne enzymy – topoizomerazy – potrafią ją rozplątać.
Jedną z metod określenia rodzaju węzła, w jaki zasupłana jest nić DNA, jest poddanie jej działaniu pola elektrycznego lub siły odśrodkowej w wirówce. Okazuje się, że pod działaniem zewnętrznej siły pętle z DNA przesuwają się z różnymi prędkościami w zależności od ich topologii. Skąd bierze się ten nieoczekiwany związek? Badań tego problemu podjęły się Magdalena Gruziel i Maria Ekiel-Jeżewska (z Instytutu Podstawowych Problemów Techniki PAN) we współpracy z Piotrem Szymczakiem (z Wydziału Fizyki Uniwersytetu Warszawskiego) oraz Giovannim Dietlerem, Andrzejem Stasiakiem i , Krishnanem Thyagarajanem z Lozanny. Aby lepiej zrozumieć ten nieoczekiwany związek pomiędzy topologią a dynamiką DNA zaprojektowali oni eksperyment w skali makro, w którym rolę zawęźlonych nici DNA odgrywały łańcuszki ze stalowych kulek. Jako płynu użyto bardzo lepkiego oleju silikonowego, aby charakter przepływu wokół kilkucentymetrowego łańcuszka buł analogiczny do przepływu wokół mikroskopowej pętli DNA w wodzie.
Zachowanie łańcuszków wrzuconych do lepkiej cieczy okazało się zaskakujące. Ich ruch bardzo przypominał zachowanie kółek z dymu Taita i Kelvina. Łańcuszki rozpłaszczały się, tworząc cienki torus w płaszczyźnie prostopadłej do kierunku grawitacji. Torus ten złożony był z jednej lub więcej splecionych ze sobą pętli, nieustannie wirujących wokół siebie. Dodatkowo, cały torus obracał się dookoła swojej osi, w kierunku określonym przez skrętność węzła.
 |
Aby wyjaśnić to zaskakujące zachowanie opadających pętli, autorzy pracy z Physical Review Letters stworzyli model teoretyczny elastycznych włókien poruszających się w lepkiej cieczy, a następnie przeprowadzili symulacje numeryczne ich ruchu, które w pełni odtworzyły dynamikę obserwowaną w eksperymencie i powinny także stosować się do opisu dynamiki hydrodynamicznie podobnych obiektów w mikroskali. Modelowanie matematyczne pozwoliło na ustalenie, że skoordynowany ruch pętli powstaje dzięki tak zwanym oddziaływaniom hydrodynamicznym pomiędzy różnymi częściami łańcucha. Każdy element łańcuszka, przesuwając się, wywołuje przepływ otaczającego płynu, który działa na wszystkie inne elementy łańcucha. Właśnie te oddziaływania przenoszone przez przepływ sprzęgają ze sobą ruch pętli i sprawiają, że zaczynają one wirować względem siebie. Charakterystyki ruchu wirowego łańcuszków zależą od ich długości oraz sztywności. Co ciekawe, można też pokazać, że wiry Kelvina i Taita, jeśli zapleść je w węzeł, wykonywałyby ruch zupełnie analogiczny do obserwowanego w eksperymentach z łańcuszkami. |
| Zawęźlone pętle opadające w lepkiej cieczy: eksperyment (z lewej) i symulacja komputerowa (z prawej) – Phys. Rev. Lett. 121, 127801. (2018). |
Najistotniejszy wynik tej pracy – pokazanie, że giętkie pętle z węzłami o skomplikowanej topologii opadając w ośrodkach płynnych mogą tworzyć uporządkowane, niemal płaskie toroidalne struktury – jest ważny dla właściwej interpretacji eksperymentów sedymentacji DNA i innych biomolekuł, o których zwykle dotychczas zakładało się, że pod wpływem siły grawitacji opadają w postaci nieuporządkowanego kulistego kłębka.
M. Gruziel, K. Thyagarajan, G. Dietler, A. Stasiak, M. L. Ekiel-Jezewska, P. Szymczak, Periodic motion of sedimenting flexible knots, Physical Review Letters, 121, 127801. (2018) – patrz tutaj
Komentarz American Physical Society – patrz tutaj











